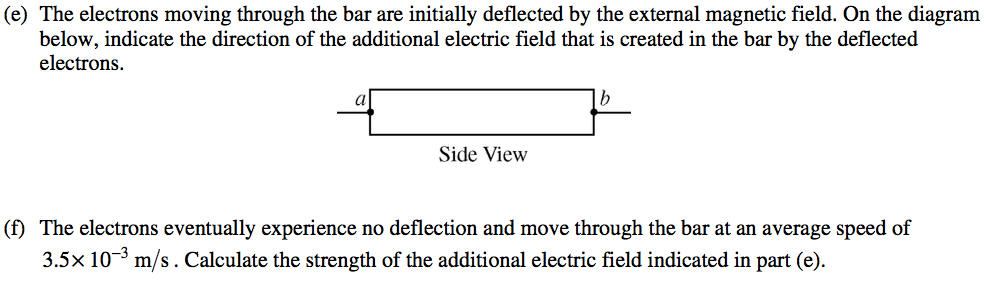
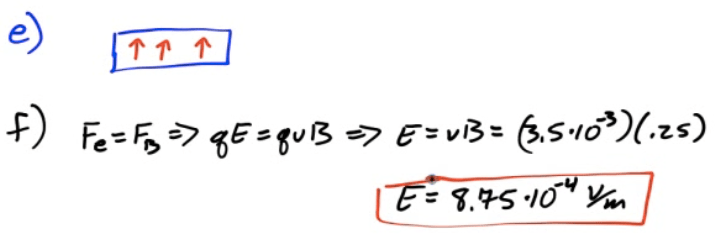Example 1: Torque on a Loop of Wire
A loop of wire carrying current I is placed in a magnetic field. Determine the net torque around the axis of rotation due to the current in the wire.
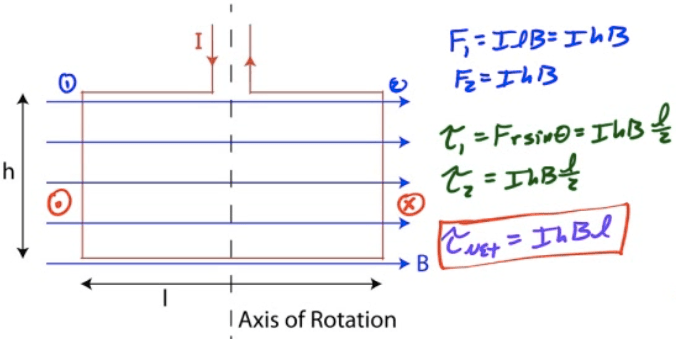
Magnetic Field due to a Current-Carrying Wire
Moving charges create magnetic fields
Current-carrying wires carry moving charges, therefore they create B fields
Direction given by right-hand rule
For multiple wires, determine B field from each and add them up using superposition
B fields may interact with other moving charges, so current-carrying wires can exert forces upon each other.
First Right Hand Rule
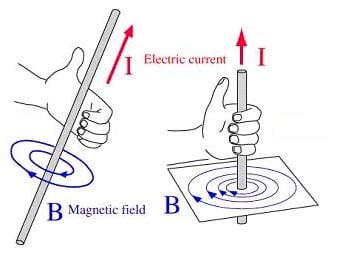
"Hold" wire with your right hand, thumb in direction of positive current flow
Your fingers wrap in the direction of the magnetic field
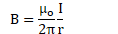
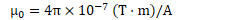
Example 2: Magnetic Field due to a Wire
A wire carries a current of 6 amperes to the left.
Find the magnetic field at point P, located 0.1 meters below the wire
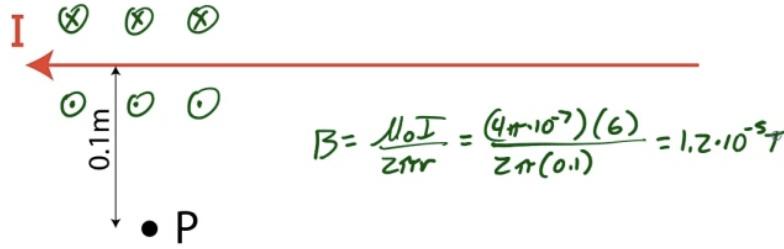
Force Between Parallel Current-Carrying Wires
Use right hand rules to determine force between parallel current-carrying wires
Find magnetic field due to first wire. Draw it.
Find direction of force on second wire due to current in second wire. Force on the first wire will be equal and opposite (Newton's third Law)

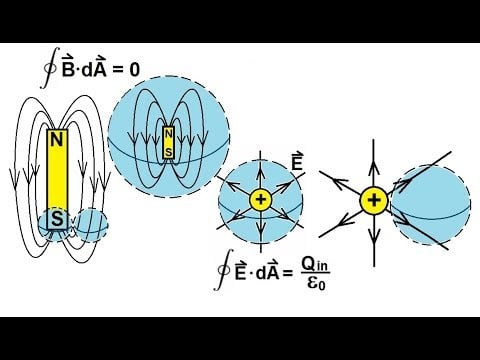
Gauss's Law for Magnetism
You can never draw a closed surface with any net magnetic flux because there are no magnetic monopoles.
This is the basis of Gauss's Law for Magnetism (Maxwell's second equation)
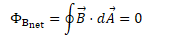
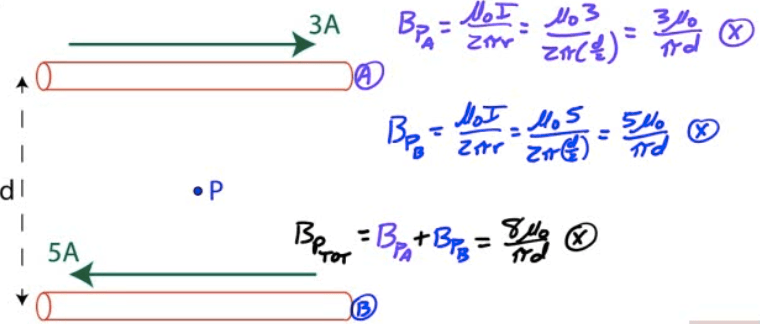
Example 3: Field due to Wires
Two long current-carrying wires are separated by a distance d as shown.
What is the net magnetic field due to these wires at point P, located midway between the two wires, if the top wire carries a current of 3A and the bottom wire caries a current of 5A.
Example 4: Force on a Wire
A 5-m long straight wire runs at a 45-degree angle to a uniform magnetic field of 5 T. If the force on the wire is 1N, determine the current in the wire
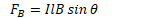
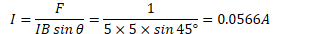
2009 Free Response Question 2

![Eş\!\!\] z 72-2 z : 3 (2 u 22 91 • S •](media/image394.png)